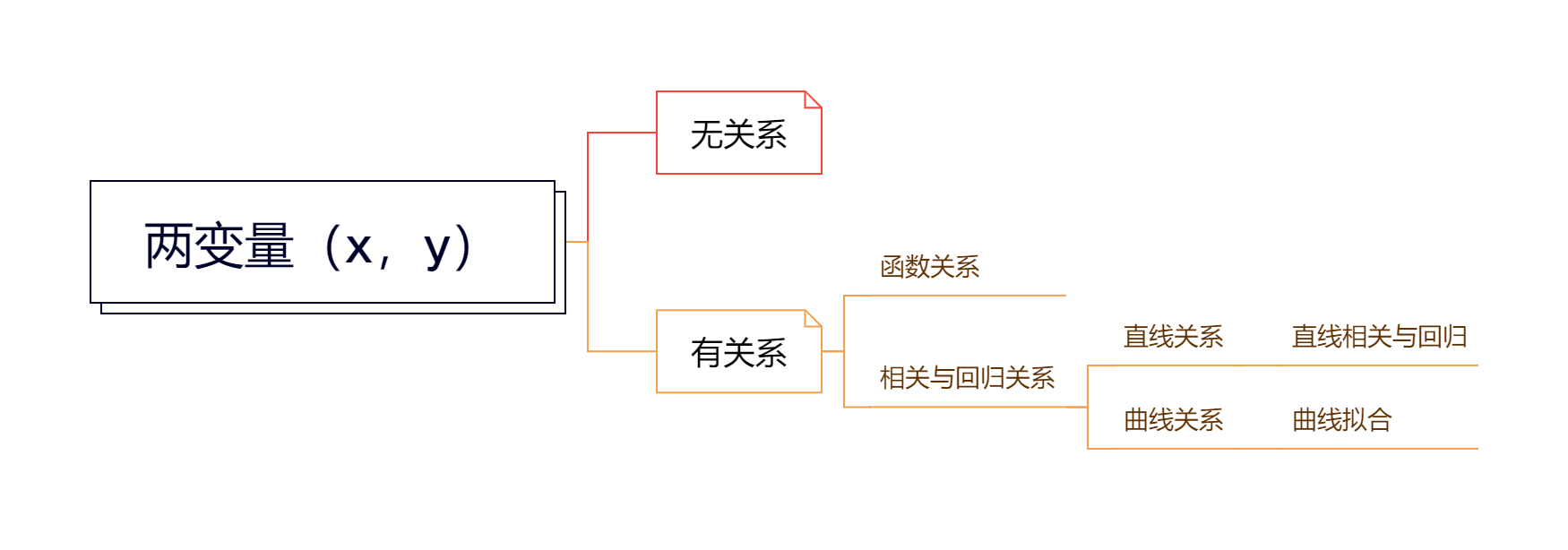
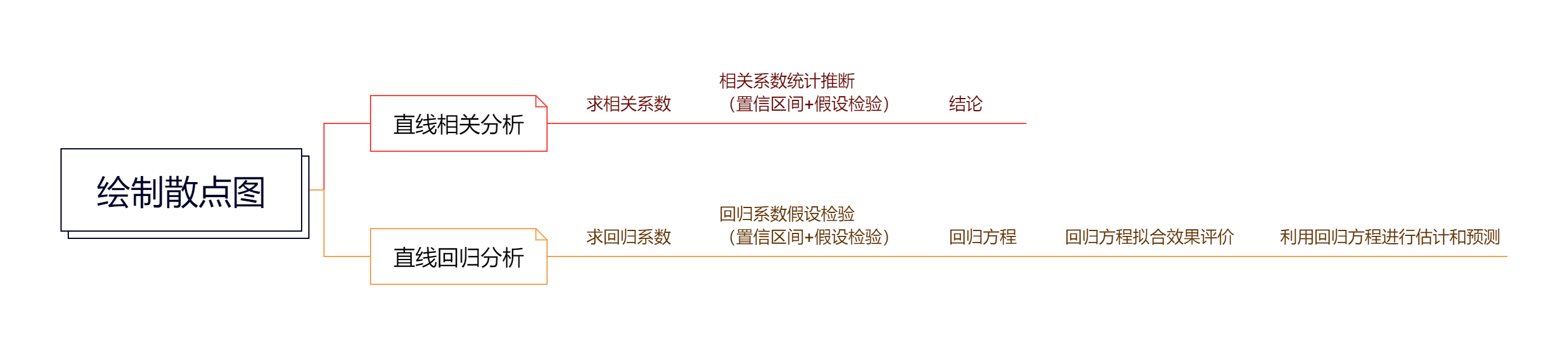
Chapter 14 简单线性相关和回归
14.3 简单直线回归
14.3.2 回归方程的建立
选择一组数据集的“最佳拟合直线”,需要设法通过观测数据确定参数\(\alpha\)与\(\beta\)的估计值a和b,使得直线
\[\hat y=a+bx\]
能最佳地反映\((x_i,y_i)\)之间的变化关系,该直线称为一元回归直线。
常用最小二乘估计法(least squares estimation)来最佳直线,其基本原理是通过最小化残差平方和,使得各观测点到回归直线的纵向距离的平方和最小。
\[ \begin{cases} a=\bar y-b \bar x\\ b=\frac{\sum\limits_{i=1}^n x_i y_i - \frac{1}{n}(\sum\limits_{i=1}^n x_i)(\sum\limits_{i=1}^n y_i)}{\sum\limits_{i=1}^n x_i^2 - \frac{1}{n}(\sum\limits_{i=1}^n x_i)^2} \end{cases} \] 为方便,引入以下记号: \[ SS_{xx}=\sum_{i}(x_i-\bar x)^2=\sum_{i}x_i^2-\frac{1}{n}(\sum_{i}x_i)^2\\ SS_{yy}=\sum_{i}(y_i-\bar y)^2=\sum_{i}y_i^2-\frac{1}{n}(\sum_{i}y_i)^2\\ SS_{xy}=\sum_{i}(x_i-\bar x)(y_i-\bar y)=\sum_{i}x_i y_i-\frac{1}{n}(\sum_{i}x_i)(\sum_{i}y_i) \] 其中,\(SS_{xx}\)和\(SS_{yy}\)是离均差平方和,\(SS_{xy}\)称为离均差积和。
这样可以简化为: \[ \begin{cases} a=\bar y-b \bar x\\ b=\frac{SS_{xy}}{SS_{xx}} \end{cases} \]
14.3.3 假设检验
- F检验
\(y_i\)的总离均差平方和为:
\[SS_{yy}=\sum_{i}(y_i-\bar y)^2\] 对其做分解,得到等式:
\[SS_{yy}=\sum_{i}^{n}(\hat y_i-\bar y)^2+\sum_{i}^{n}(y_i-\hat y_i)^2\] \(\sum_{i}^{n}(\hat y_i-\bar y)^2\)为回归平方和(regression sum of squares),记为\(SS_R\),表示回归估计值\(\hat y_i\)与均数\(\bar y\)的离差平方和,其公式为:
\[ \begin{align} SS_{yy} &= \sum_{i=1}^{n}(\hat y_i - \bar y)^2 \\ &= \sum_{i=1}^{n}[a + bx_i - (a + b\bar x)]^2 \\ &= SS_{xx}b^2 \\ &= SS_{xy}b \end{align} \] 显然,回归平方和\(SS_{R}\)反映的是在y的总变异中由x与y的直线回归关系解释的那部分变异。\(SS_R\)值越大,说明回归直线的拟合效果就越好。
\(\sum_{i}^{n}(y_i-\hat y_i)^2\)为残差平方和(residual sum of squares),记为\(SS_E\),表示观测值\(y_i\)与回归估计值\(\hat y_i\)的离差平方和,其公式为: \[SS_E=\sum_{i=1}^{n}(y_i-\hat y_i)^2\] \(SS_E\)反映了在总变异中扣除自变量x对因变量y的线性影响以后的其他因素(包括x对y的非线性影响和随机误差等)对y变异的影响,也就是在总平方和中无法用y和x线性回归关系解释的部分。\(SS_E\)值越小,说明回归直线的拟合效果就越好。
对公式进行简化: \[\begin{align} SS_{yy}=&\sum_{i}^{n}(\hat y_i-\bar y)^2+\sum_{i}^{n}(y_i-\hat y_i)^2\\ =&SS_R+SS_E \end{align}\] 上述三个平方和,各有其相应的自由度\(v\),并有如下关系: \[v_{yy}=v_R+v_E\\ v_{yy}=n-1,v_R=1,v_E=n-2\]
在\(H_0\)成立的条件下,有: \[\frac{SS_R}{\sigma^2}\sim \chi^2(v_R),\frac{SS_E}{\sigma^2}\sim \chi^2(v_E)\] 且\(SS_R\)和\(SS_E\)相互独立。
检验统计量:
\[F=\frac{SS_R/v_R}{SS_E/v_E}\] 服从自由度\(v_R=1,v_E=n-2\)的F分布。如果y和x确实存在直线回归关系,那么回归所解释的变异\(SS_R\)应大于其他因素所解释的变异\(SS_E\)。由此可见,F检验正是建立在这个基础上的。
对于给定的检验水准\(\alpha\), 如果\(F>F_{(v_R,v_E),1-\alpha}\),则拒绝\(H_0\),认为直线回归方程有统计学显著性;
如果\(F\leq F_{(v_R,v_E),1-\alpha}\),则不拒绝\(H_0\),尚不能认为直线回归方程有统计学显著性。
- t检验法
14.4 直线相关与直线回归的比较
| 区别与联系 | 类目 | 内容 |
|---|---|---|
| 区别 | 资料要求 | 1. 线性相关要求X,Y服从双变量正态分布,对这种资料进行回归分析称为\(\textrm{II}\)型回归,即可以把X当自变量,也可以当因变量,反之亦然。 2. 线性回归要求Y在给定X值时服从正态分布,X可以是精确测量和严格控制的变量,这时的回归称为型回归,即不可以把X当因变量,Y当自变量进行回归分析。 |
| 应用 | 1. 线性相关用来表达两个变量间的互依关系,两个变量的研究地位是相等的,谁做X,谁做Y都可以; 2. 线性回归用来表达两个变量间的依存变化的数量关系,即一个变量(为因变量Y)如何依存于另一个变量(为自变量X)而变化,两个变量的研究地位是不相等的。 |
|
| 意义 | 1. 相关系数r说明具有线性关系的两个变量之间的密切程度和相关方向; 2. 回归系数b表示X每变化一个单位所导致的Y的平均变化量。 |
|
| r和b的取值范围 | r没有单位,而b有单位(其单位是:Y的单位/X的单位),所以导致两者的取值范围不同; \(-1 \le r \le 1\),\(-\infty<b<+\infty\) |
|
| r和b的计算公式不同 | \(r=\frac{l_{xy}}{\sqrt{l_{xx}l_{yy}}}\),\(b=\frac{l_{xy}}{l_{xx}}\) | |
| 联系 | 符号 | 对于既可以做相关又可作回归的同一组资料,计算出r与b的正负号相同 |
| 假设检验 | 对于同一组资料,相关系数和回归系数的假设检验等价。即有:\(t_b=t_r\) | |
| 相互换算 | 对于同一组资料,相关系数和回归系数可通过下式换算:\(b=s\frac{S_Y}{S_X}\), 式中的\(S_X,S_Y\)分别是\(X,Y\)的标准差 |
|
| 用回归解释相关 | 又决定系数\(R^2=\frac{SS_{回}}{SS_{总}}\),当总平方和的大小决定了相关的密切程度,回归平方和越接近总平方和,则\(R^2\)越接近1,相关的效果越好,说明回归效果越好,相关的密切程度也越高。 |
notice:关于双变量正态分布
双元正态变量是指两个随机变量同时遵循正态分布的情况,通常记作 \((X, Y) \sim N(\mu, \Sigma)\),其中 \(\mu\) 是均值向量,\(\Sigma\) 是协方差矩阵。
数学定义
1. 均值向量:对于双元正态变量 $(X, Y)$,均值向量为:\[\mu = \begin{pmatrix} \mu_X \\ \mu_Y \end{pmatrix}\]
其中 \(\mu_X\) 和 \(\mu_Y\) 分别是随机变量 \(X\) 和 \(Y\) 的均值。 2. 协方差矩阵:协方差矩阵为:
\[\Sigma = \begin{pmatrix} \sigma_X^2 & \sigma_{XY} \\ \sigma_{XY} & \sigma_Y^2 \end{pmatrix}\]
其中 \(\sigma_X^2\) 和 \(\sigma_Y^2\) 是 \(X\) 和 \(Y\) 的方差,\(\sigma_{XY}\) 是它们之间的协方差。
性质
• 边缘分布:$X$ 和 $Y$ 的边缘分布也是正态分布。
• 条件分布:给定 $X$ 的值,$Y$ 的条件分布也是正态分布。
• 相关性:协方差矩阵的值可以用来判断 X 和 Y 之间的相关性。如果 $\sigma_{XY} > 0$,则两者正相关;如果 $\sigma_{XY} < 0$,则负相关。示例
假设有一组数据描述学生的身高 \(X\) 和体重 \(Y\),并且假设 \((X, Y)\) 服从双元正态分布:
• 均值向量:\[\mu = \begin{pmatrix} 170 \\ 65 \end{pmatrix}\]
表示身高的均值为 170 厘米,体重的均值为 65 千克。 • 协方差矩阵:
\[\Sigma = \begin{pmatrix} 100 & 20 \\ 20 & 25 \end{pmatrix}\]
这里,身高的方差为 100,体重的方差为 25,协方差为 20,表示身高和体重之间存在正相关关系。
在这个示例中,如果我们知道某个学生的身高为 180 厘米,我们可以利用条件分布来预测他的体重,这个体重的预测值也是正态分布。
我们用一个图形来展示:
## 安装和加载所需的包
#install.packages("plotly")
#install.packages("mvtnorm")
#library(plotly)
#library(mvtnorm)
# 创建网格数据
x <- seq(150, 190, length.out = 100)
#身高150-190,等距的100个值
y <- seq(50, 80, length.out = 100)
#体重50-80,等距的100个值
grid <- expand.grid(X = x, Y = y)
#生成 x 和 y 的所有组合,用于构建一个网格数据框,以便计算多元正态分布的概率密度。
# 设置均值和协方差矩阵
mu <- c(170, 65)
#设置双元正态分布的均值向量,表示均值分别为身高 170 cm 和体重 65 kg
sigma <- matrix(c(100, 20, 20, 25), nrow = 2)
#设置协方差矩阵,表示身高的方差为 100,体重的方差为 25,身高和体重之间的协方差为 20
# 计算概率密度
z <- dmvnorm(as.matrix(grid), mean = mu, sigma = sigma)
#计算每个网格点上双元正态分布的概率密度。
# 将概率密度矩阵转换为适合绘图的形状
z_matrix <- matrix(z, nrow = 100, ncol = 100)
# 绘制三维表面图
plot_ly(x = x, y = y, z = z_matrix, type = "surface") %>%
layout(title = list(text = "双元正态分布的三维概率密度图", y=0.95),
scene = list(xaxis = list(title = "身高 (cm)"),
yaxis = list(title = "体重 (kg)"),
zaxis = list(title = "概率密度")))Figure 14.1: Binary normal distribution