Chapter 3 不同资料的统计描述
3.1 定量资料的描述指标
3.1.1 集中趋势指标
| 指标 | 定义→本质 | 表示方法 | 计算方法 | 应用条件 |
|---|---|---|---|---|
| 算术均数 | 先求和再平均 | (1)样本均数:\(\bar x\) (2)总体均数:\(\mu\) |
(1)直接法:\(\bar X=\frac{\sum{X_{i}}}{n}\) (2)加权法:\(\bar X = \frac{\sum{f_{i}X_{i}}}{\sum{f}}\), (\(X\)为组中值,\(f\)为频数) |
(1)对称分布,尤其是正态分布 (2)不含极端值 |
| 几何均数 | 先乘积再开方 | \(G\) | (1)直接法:\(G=\sqrt[n]{x_{1}·x_{2}·x_{3}\cdots}x_{n}\) (2)加权法:\(G=\ln^{-1}(\frac{\sum{f_{i}\ln X_{i}}}{\sum{f_{i}}})\) |
(1)数据呈倍数变化或对数正态分布→正偏态分布 (2)观察值中不能有零且不能同时有正数和负数→对数性质 |
| 中位数 | 从小到大找中间 还要注意奇偶性 |
\(M\) | (1)直接法:n为奇数,\(M=X_{\frac{n+1}{x}}\) n为偶数,\(M=\frac{1}{2} (X_{\frac{n}{2}}+X_{\frac{n}{2}+1})\) (2)加权法:百分位数法\(P_{X}=L_{X}+\frac{i}{f_{x}}(nX\%-\sum{f_{i}})\) |
任何资料 |
| 众数 | 出现次数最多 | \ | (1)直接法:一组数据中出现次数最多的数值 加权法:f最多的组段的组中值\(X\) |
任何数据 |
3.2 离散数据的描述指标
3.2.1 离散趋势指标
| 指标 | 本质→定义 | 表示方式 | 计算公式 | 适用条件 |
|---|---|---|---|---|
| 极差 | \(X_{Max}-X_{Min}\) | \(R\) | ||
| 四分位间距/范围 | 位置指标 | \(IQR\) | \(IQR=P_{75}-P_{25}\) | 任何资料 |
| 方差 | 离均差平方和求平均 | 样本:\(s^{2}\) 总体:\(\sigma^{2}\) |
\(s^{2}=\frac{\sum(x_{i}-x)^2}{(n-1)}\) | 对称分布,尤其是正态分布;不含极端值 |
| 标准差 | 方差开根号 | 样本:\(s\) 总体:\(\sigma\) |
\(s=\sqrt{\frac{\sum(x_{i}-x)^2}{(n-1)}}\) | 同上 |
| 变异系数 | 测量数据变异程度的相对统计量 | \(CV\) | \(CV=\frac{s}{\bar x}×100%\) | (1)单位相同:但均数相差悬殊; (2)单位不同 |
3.2.2 标准差(standard deviation)的计算
- 直接法 \[s=\sqrt{\frac{\sum\limits_{i=1}^nx_i^2-\frac{\left(\sum\limits_{i=1}^nx_i\right)^2}{n}}{n-1}}\]
- 加权法:与讨算均数的方法类似,对频数表资料采用加权法,讨算公式为
\[s=\sqrt{\frac{\sum\limits_{k=1}^gf_kx_{mk}^2-\left(\sum\limits_{k=1}^gf_kx_{mk}\right)^2 \left(\sum\limits_{k=1}^gf_k\right)}{\sum\limits_{k=1}^gf_k-1}}\]
3.3 分类资料的描述指标
3.3.1 分类资料的统计描述指标
| 指标 | 相对比 | 构成比 | 频率型指标 | 强度性指标 |
|---|---|---|---|---|
| 定义 | 两个有关联的指标之比 | 某一部分与总体之比 | 某时期内累计出现的频率 | 单位时间内某件事发生的频率 |
| 计算公式 | \(\frac{A指标}{B指标}\) | \(\frac{某一事物总体中某一部分}{某一事物所有组成部分的总体}×100\%\) | \(\frac{同时期实际发生某现象的观察单位数}{某时期可能发生某现象的观察单位总数}×K\) | \(\frac{发生某件事的观察单位数}{\sum(观察单位×观察时间)}×K\) |
| 量纲 | 可有可无 | 一般无量纲 | 无 | 有 |
| 取值 | 没有限制 | [0,1] | [0,1] | 可大于1 |
| 举例 | RR,变异系数CV | 死因构成比 | 病死率,累计发病率 | 发病率,发病密度 |
3.4 率的标准化
| 指标 | 参照人数 | 目标人群 | 过程 |
|---|---|---|---|
| 直接标化法 | 人口构成 | 率 | 各年龄组期望死亡数→期望死亡合计数→直接标化率 |
| 简介标化法 | 率 | 人口构成 | 各年龄组期望死亡数→期望死亡合计数→变化死亡比→间接标化率 |
notice:
- 变化标化比\(SMR=\frac{实际死亡人数}{期望死亡人数}\)
- 直接标准化选择的标准是:各年龄组标准人口构成比或各年龄组标准人口数
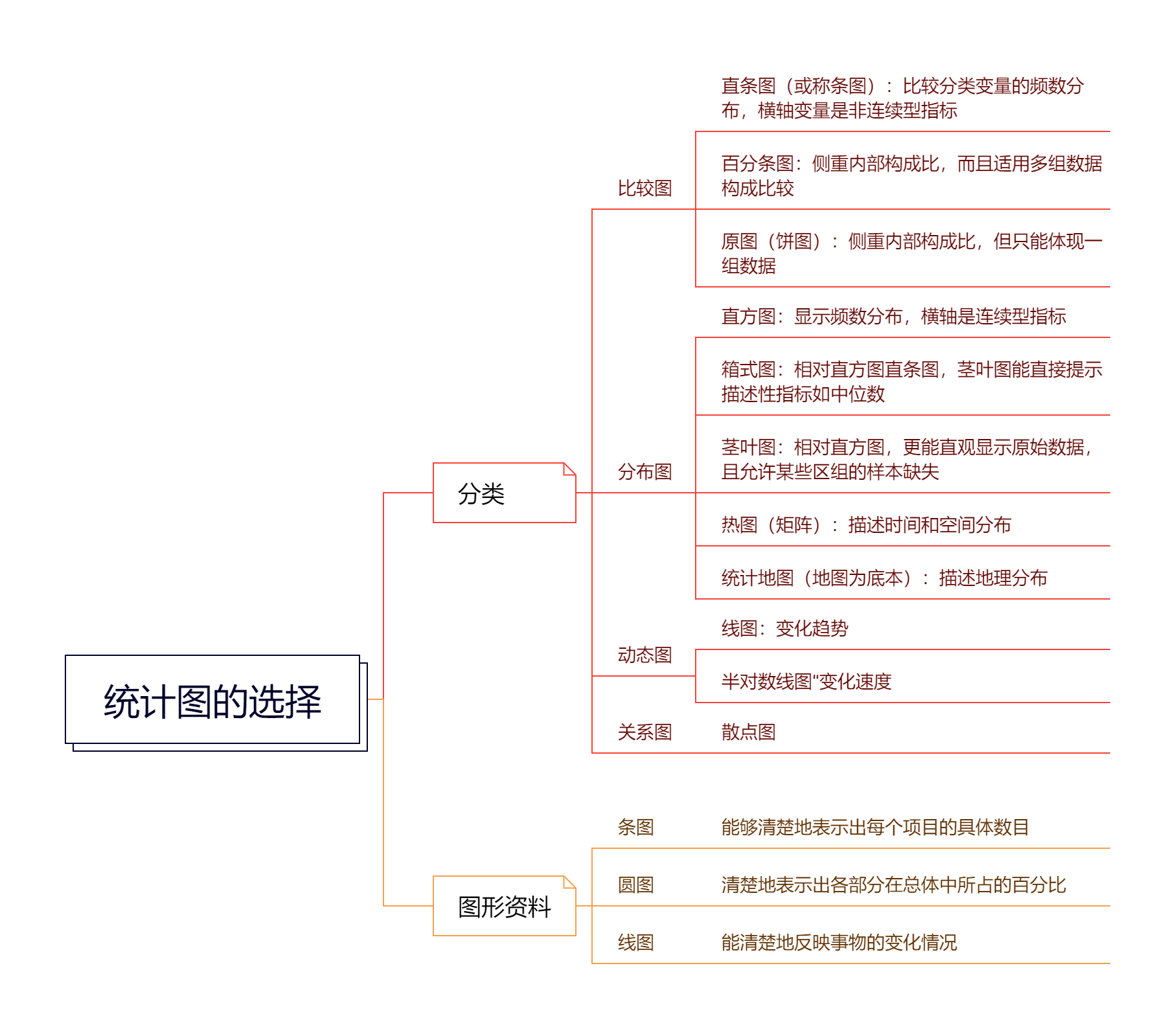
3.5 常见统计图
3.5.1 资料类型
- 连续型变量
- 计量资料
- 定量资料
- 离散型变量
- 不具有分类性质的资料
- 离散型定量资料
- 分类资料
- 有序分类资料
- 等级资料
- 半定量资料
- 无序分类资料
- 名义变量
notice:一般来说,统计图的选择,是综合考量了变量取值特点+研究目的。
3.5.2 统计图使用类型及目的
| 统计图 | 资料类型 | 分析目的 |
|---|---|---|
| 圆图和百分条图 | 构成比资料 | 用圆的扇形面积或直条各段的长度表示事物各组成部分的构成情况 |
| 直条图 | 相互独立资料 | 用直条长短表示相互独立的各指标的数值大小,一般用于比较不同组别的指标大小 |
| 直方图 | 连续型变量的频数分布 | 用矩阵面积表示各组段的频数(频率) |
| 箱式图 | 连续型资料 | 描述数据的分布特征(包括中位数、四分位范围、最大值和最小值) |
| 普通线图 | 连续型资料 | 用线段的升降表示某事物在时间上的变化趋势、或某一现象随着另一现象变化的情况 |
| 半对数线图 | 连续型资料 | 用线段的升降表示事物的相对变化速度 |
| 散点图 | 双变量连续型资料 | 表示两种事物变化的相关性和趋势 |