Chapter 7 由正态分布引出的三大抽样分布

7.1 t分布

说起t分布，首先要提一句u分布，正态分布（Normal Distribution）是许多统计方法的理论基础。

正态分布的两个参数\(\mu\)和\(\sigma\)决定了正态分布的位置和形态。为了应用方便，常将一般的正态变量X通过u变换\([(X-\mu)/\sigma]\)转化成标准正态变量u，以使原来各种形态的正态分布都转换为\(\mu=0,\sigma=1\)的标准正态分布(Standard Normal Distribution)，亦称u分布。

根据中心极限定理，通过抽样模拟试验表明，在正态分布总体中以固定 n 抽取若干个样本时，样本均数的分布仍服从正态分布，即\(N(\mu,\sigma)\)。所以，对样本均数的分布进行u变换，也可变换为标准正态分布\(N(0,1)\)。

由于在实际工作中，往往\(\sigma^2\)(总体方差)是未知的，常用\(s^2\)(样本方差)作为\(\sigma^2\)的估计值，为了与u变换区别，称为 t 变换，统计量 t 值的分布称为 t 分布。

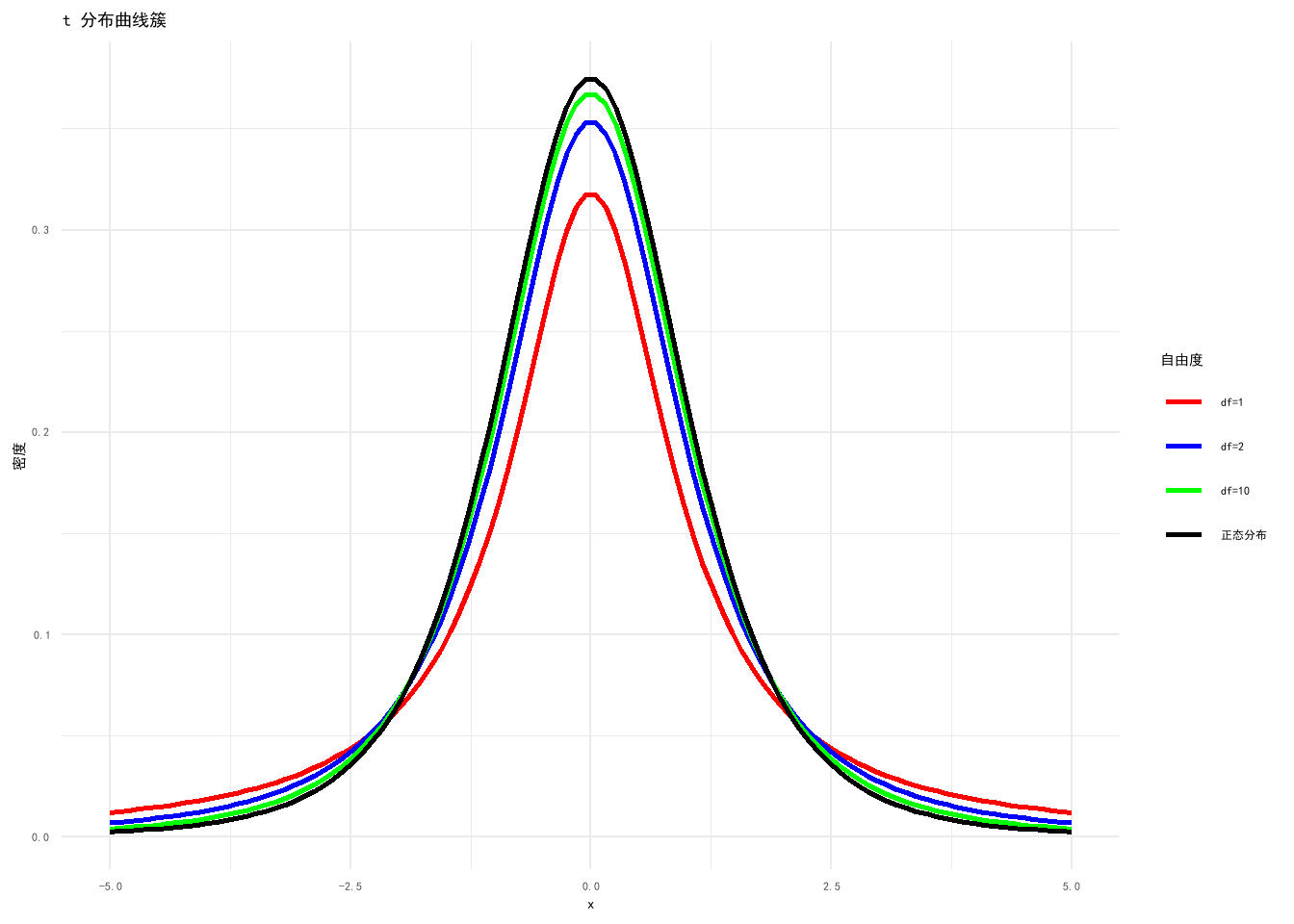
Figure 7.1: t-distribution Curves

t 分布是英国统计学家 W.S. Gosset 在 1908 年以笔名 Student发表的论文中提出的, 故后人称为 “学生氏 (Student) 分布” 或 “t 分 布”。 ## F分布

Figure 7.2: F-distribution Curves

7.1.1 F分布的应用

1. 方差的同质性检验 组与组之间的差异称组间变异（variation between classes），反映在各组的平均数不同。同一组内部被试（个体）之间的差异称组内变异（variation within class），反映在每一个个体之间的差异。
2. 总变异的分解：

• 总变异 = 组间变异+组内变异
• 组间变异 = 实验条件 + 随机误差
• 组内变异 = 个体差异 + 实验误差 。组内误差都是随机误差。

7.2 \(\chi^2\)分布

Figure 7.3: Chi-square Distribution Curves

7.2.1 卡方检验应用

1. 检验连续变量的分布是否与某种理论分布一致。
2. 检验某个分类变量各类的出现概率是否等于指定概率。
3. 检验某两种方法的结果是否一致。