Chapter 6 离散型随机变量的概率分布
6.1 二项分布(Binomial Distribution)
定义:\(n\)次伯努利试验,成功的次数为\(X\)的离散概率分布,其中每次试验的成功概率为\(\pi\),失败的概率为\(1-\pi\)。
- \(X\)的总体均数\(\mu_{x}=n\pi\)
- 总体方差\(\sigma_{x}=n\pi(1-\pi)\)
notice:
- 实际上,当\(n=1\)时,二项分布就是伯努利试验。
- 伯努利试验要求:互斥、独立、重复
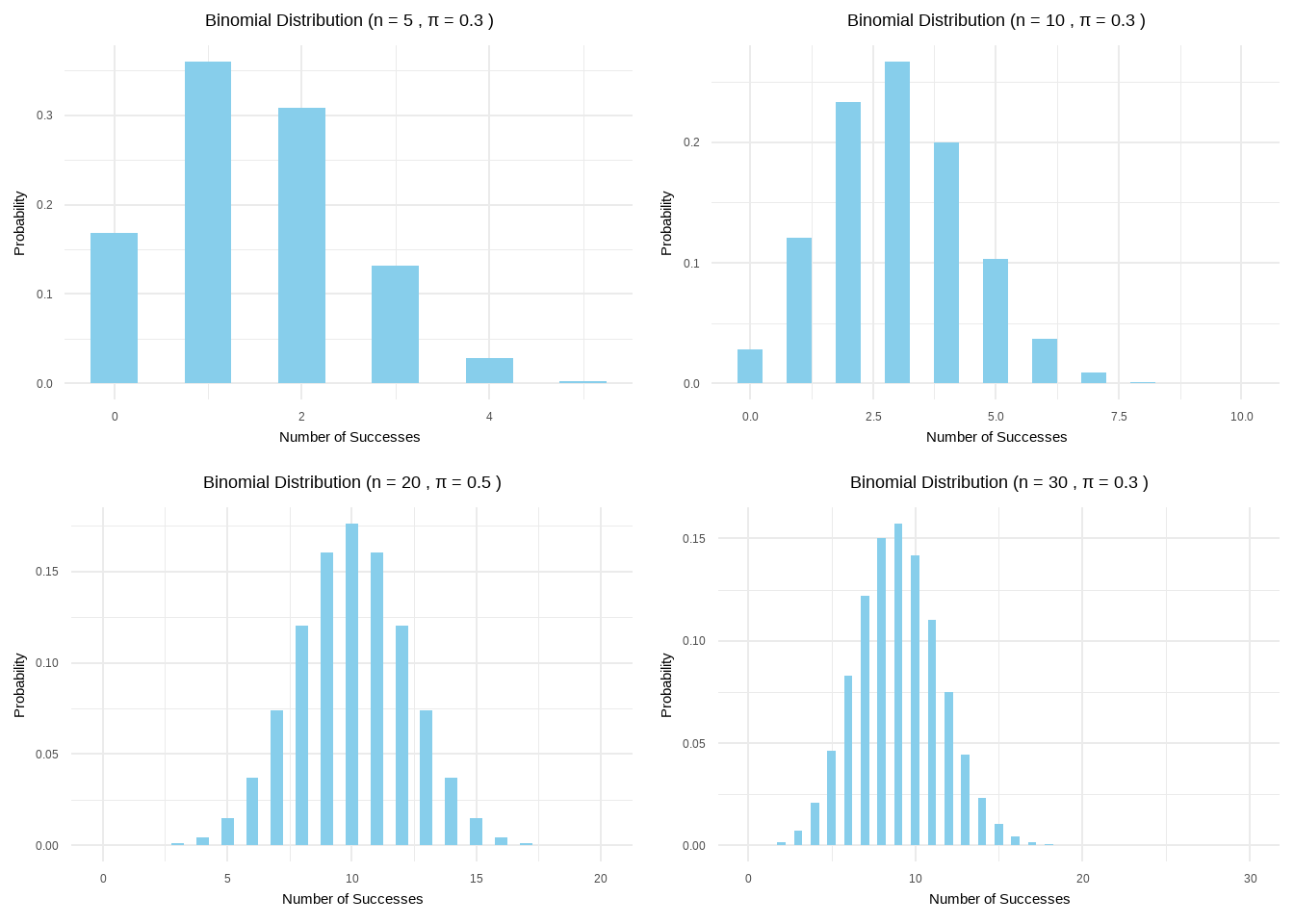
Figure 6.1: Binomial Distribution with Different n/π
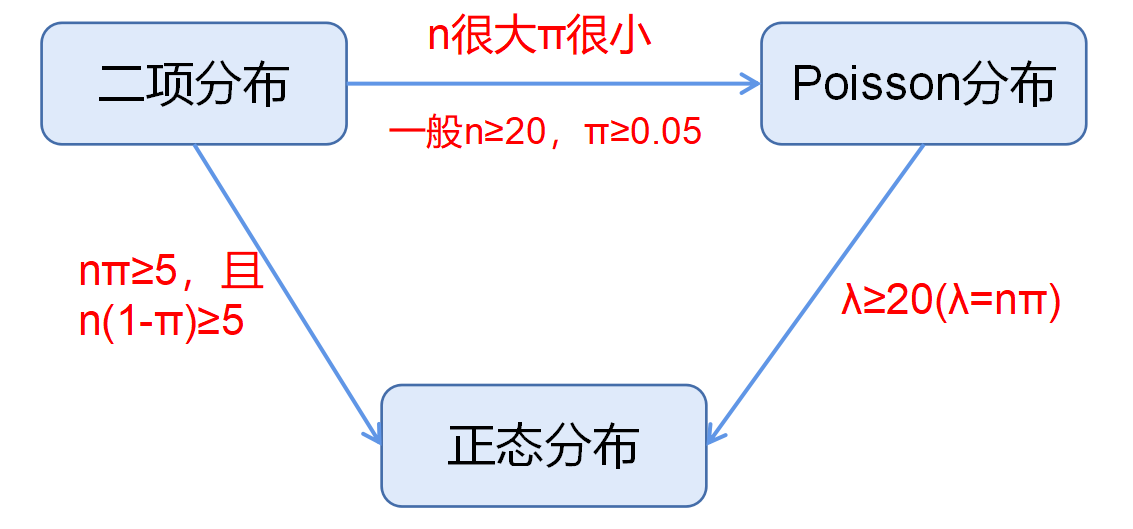
6.2 泊松分布(Poission Distribution)
定义:描述在单位面积、单位时间或单位空间中罕见事件发生次数的概率分布为泊松分布,记作\(P(\mu)\)。泊松分布是二项分布的极限形式,当一个二项分布的\(n\)很大,\(\pi\)很小时,此时,这个二项分布近似于泊松分布。
- 其总体均数与总体方差相等,记为\(\mu\)
- 可加性:\(X\sim P(\mu_{1})\),\(Y\sim P(\mu_{2})\),若\(X\)与\(Y\) 独立,则\(X+Y \sim P(\mu_{1}+\mu_{1})\)
- 泊松分布只有一个参数\(\lambda(\mu)\)
- 服从泊松分布的随机变量,其取值为\(0\)到\(+\infty\)的概率之和为1
- 一般来说,当\(\mu \ge20\)时,可以认为近似正态分布
# Define the range for x
x <- 0:40
# Define the lambda values
lambdas <- c(1, 4, 10, 20)
# Set up the plot area
plot(x, dpois(x, lambdas[1]), type="n", ylim=c(0, max(dpois(x, lambdas))),
xlab="x", ylab="Probability", main="Poisson Distribution with Different λ Values")
# Plot the Poisson distributions for each lambda
colors <- c("blue", "green", "red", "purple")
for (i in 1:length(lambdas)) {
lines(x, dpois(x, lambdas[i]), type="b", pch=19, col=colors[i])
}
# Add a legend
legend("topright", legend=paste("λ =", lambdas), col=colors, pch=19)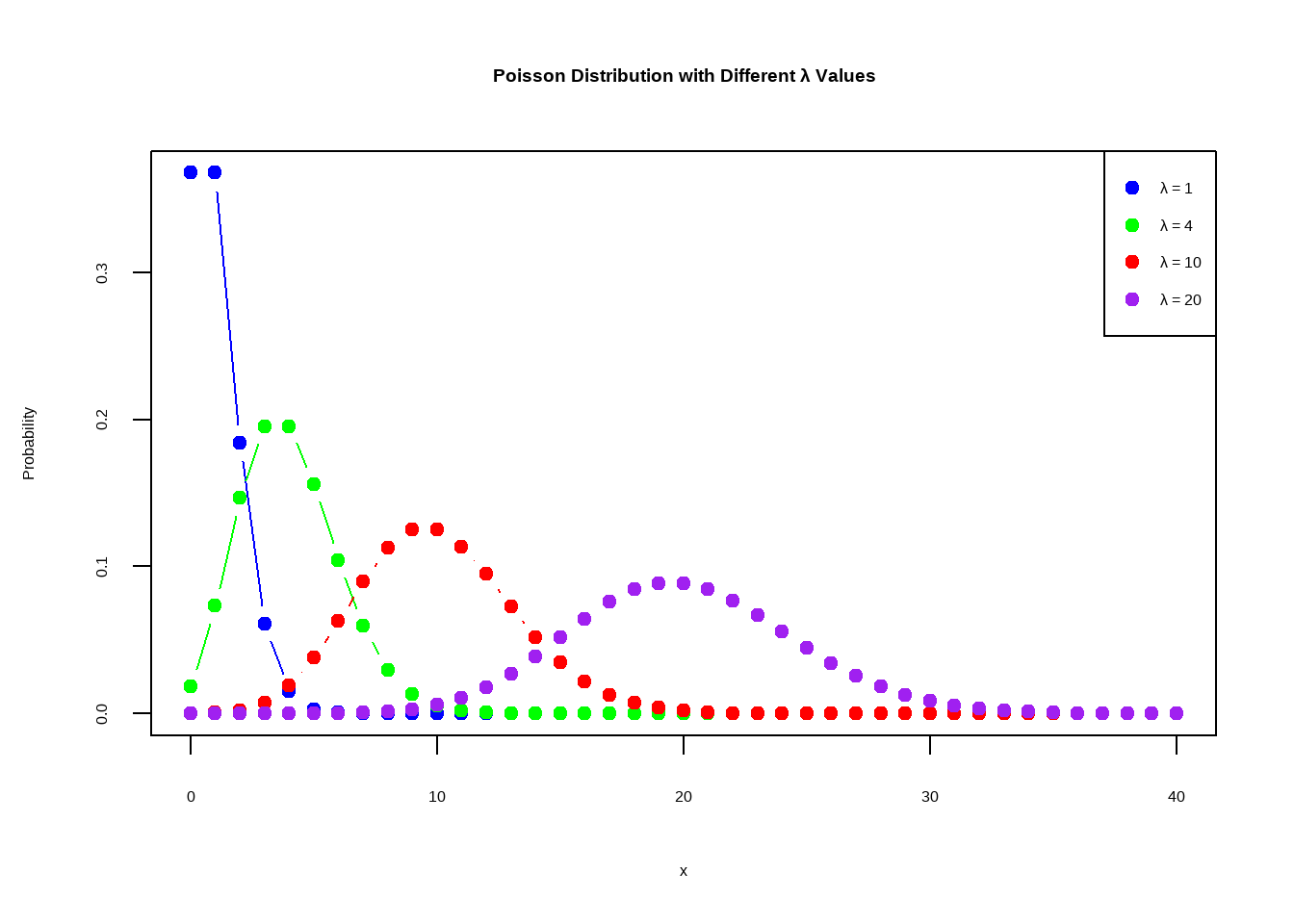
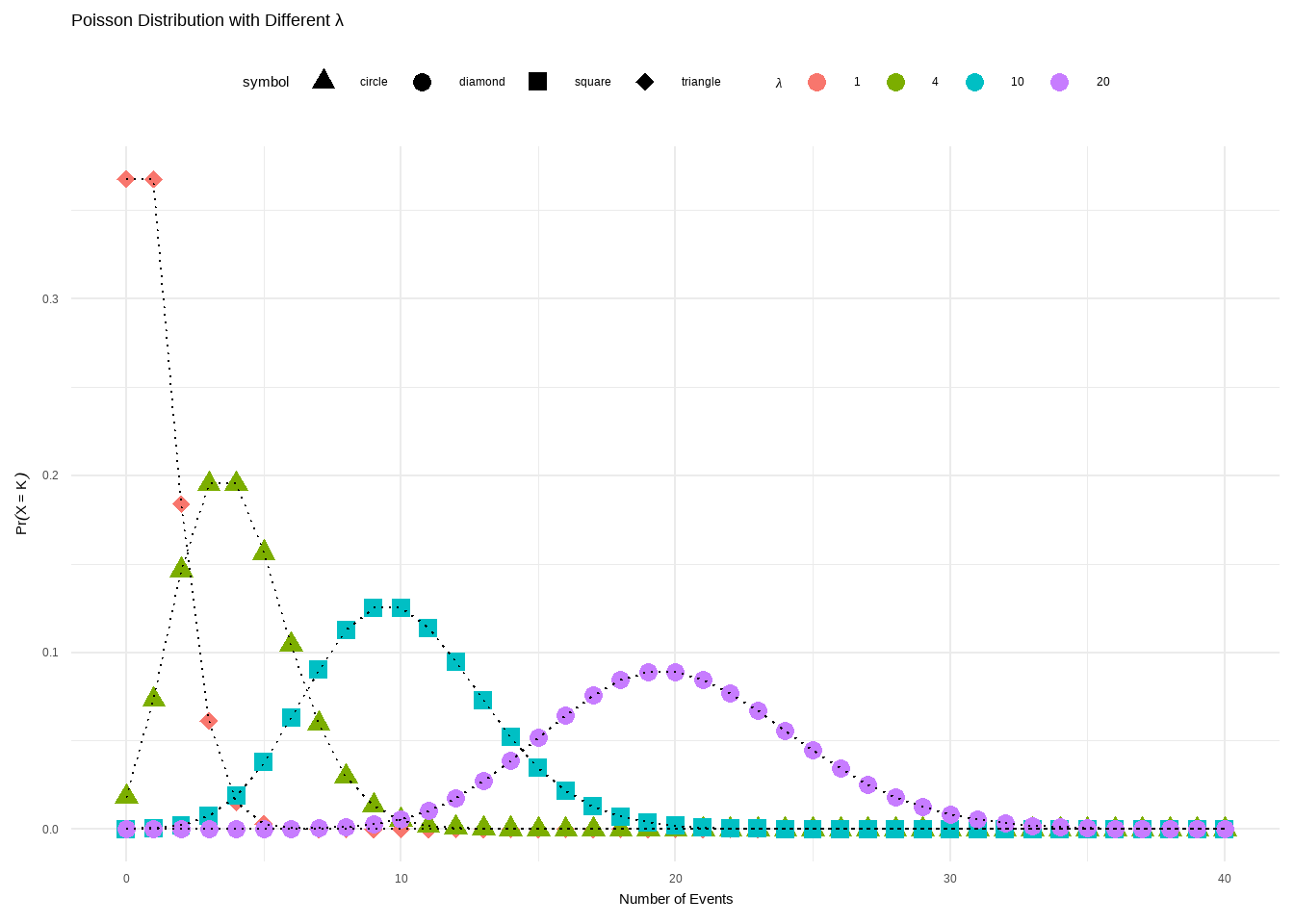
Figure 6.2: Poisson Distribution with Different λ=nπ
6.3 二项分布的应用
- 统计描述角度:直接法计算概率 \[ Pr(X=K)=\frac{n!}{k!(n-k)!}\pi^{k}(1-\pi)^{n-k},k=0,1,2,3,\cdots,n \]
- 统计推断角度:区间估计、假设检验
6.4 泊松分布的应用
- 统计描述角度:直接法计算概率 \[ Pr(X=K)=\frac{e^{-\mu}\mu^{k}}{k!},k=0,1,2,\cdots \]
- 统计推断角度:区间估计、假设检验
library(ggplot2) library(cowplot) # 连续型随机变量的概率分布
6.5 正态分布(Normal Distribution)
6.5.1 正态分布的概念
若随机变量X的密度函数是
\[f(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, (-\infty<x<+\infty)\] 则称X服从正态分布,记为\(X\sim N(\mu,\sigma^2)\)。
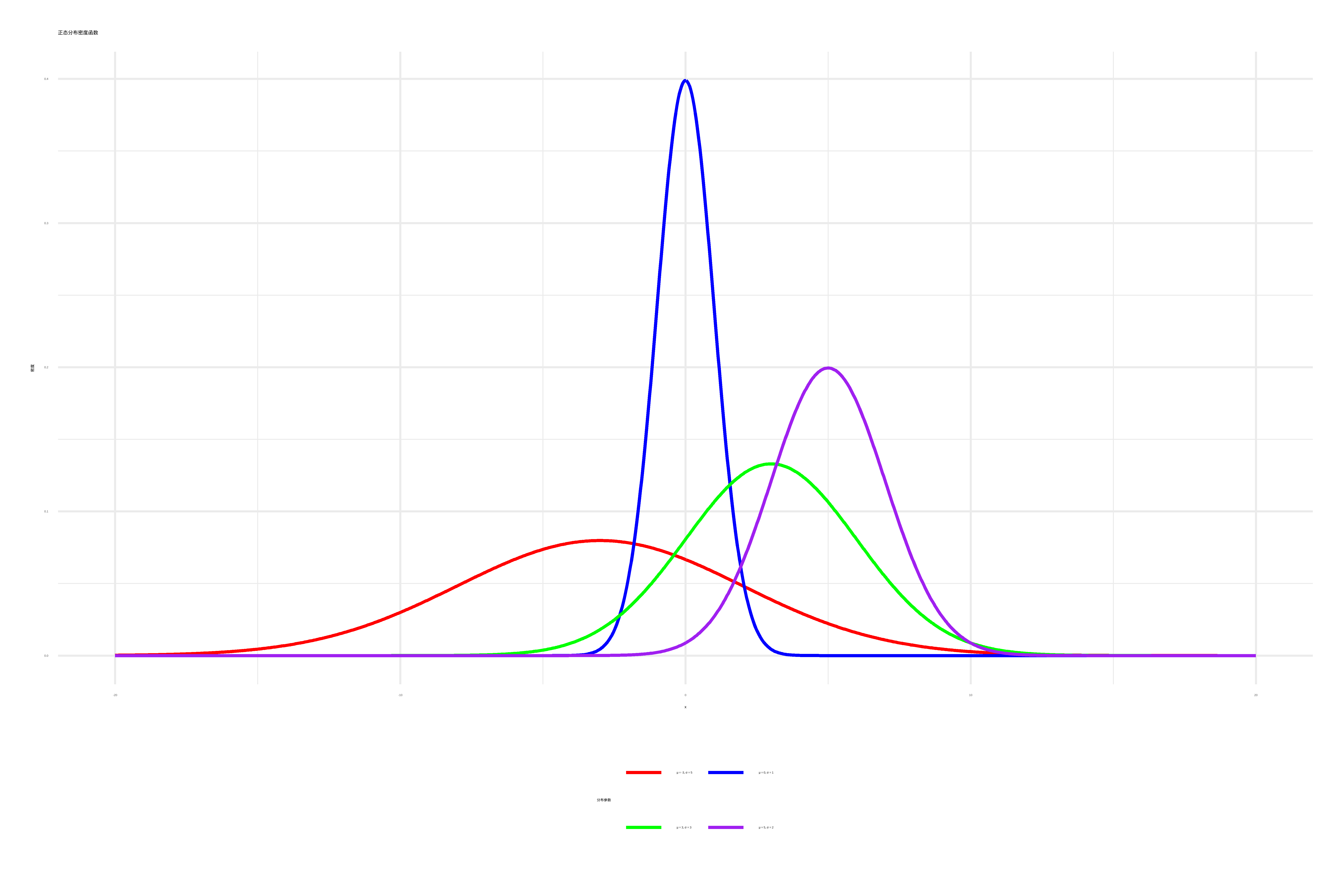
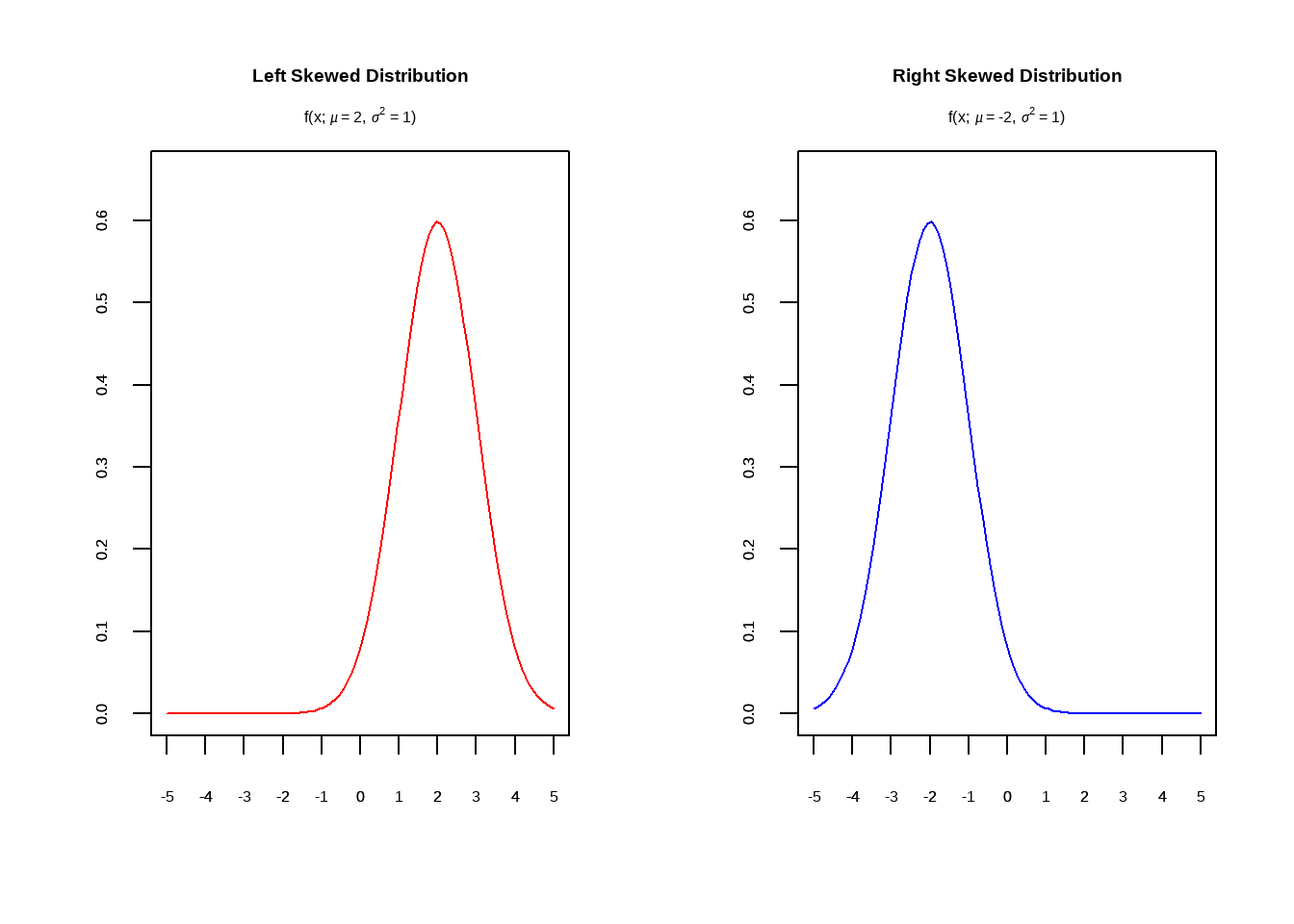
Figure 6.3: Normal Curve comparsion
- 正态分布(Normal Distribution):正态分布是最重要的连续型分布,随机变量\(X\)服从均数为\(\mu\),标准差为\(\sigma\)的正态分布,记为\(X\sim N(\mu,\sigma^{2})\)。
- 正态曲线(Normal curve):即正态分布曲线,\(\mu\)和\(\sigma\)是正态分布的两个参数。
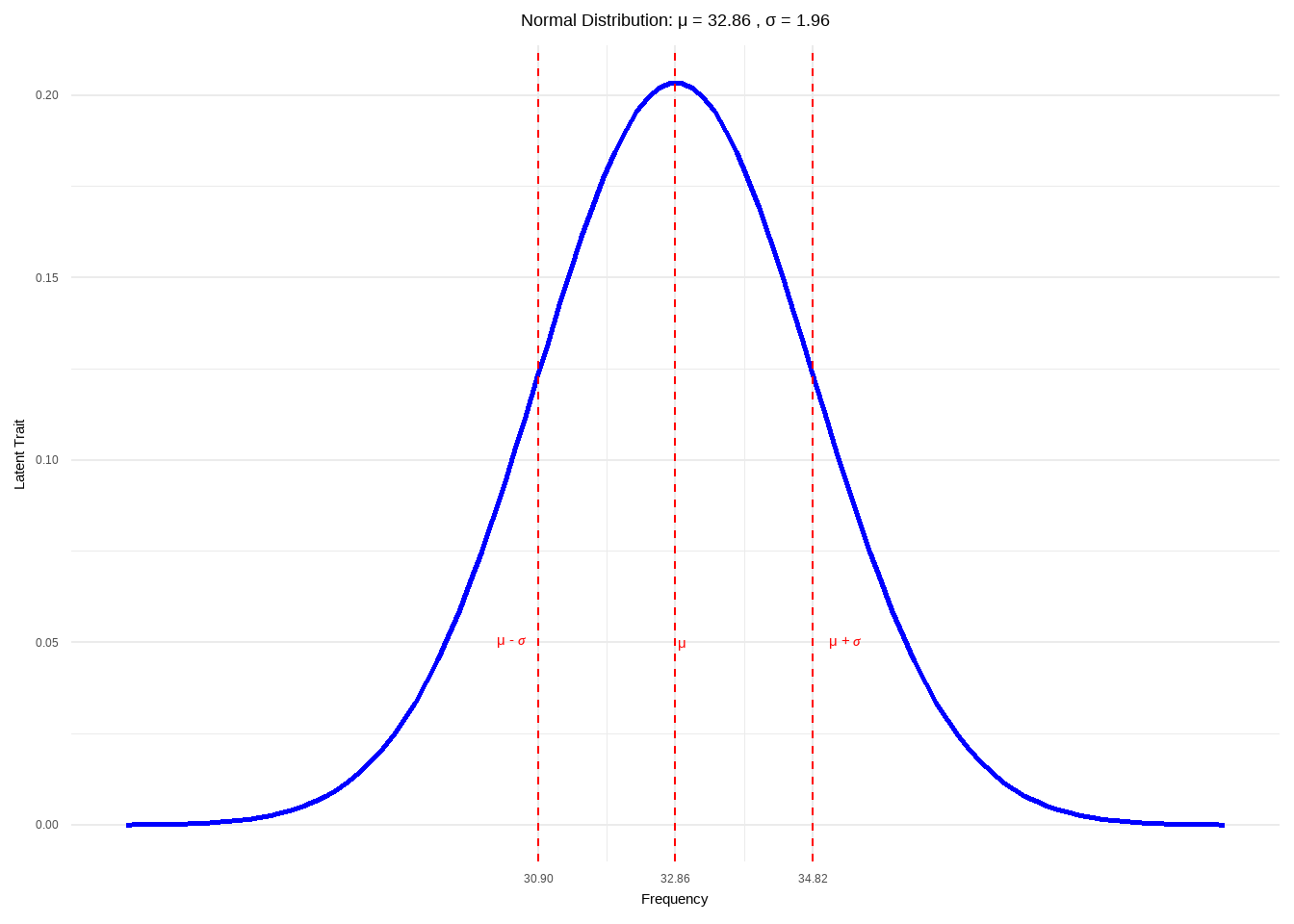
Figure 6.4: Normal Curve
- 性质
- 正态曲线在横轴上方均数处最高
- 正态分布以均数为中心,左右对称
- 正态分布有两个参数,即位置参数\(\mu\)和形态参数\(\sigma\)
- 固定\(\sigma\),改变\(\mu\)值,形态不变,曲线沿着\(X\)轴平行移动
- 固定\(\mu\),改变\(\sigma\)值,中心在\(X\)轴的位置不变
- \(\sigma\)越小,曲线越陡峭\(\to\)瘦高
- \(\sigma\)越大,曲线越低平\(\to\)矮胖
- 正态分布的可加性,当随机变量X服从正态分布\(N(\mu_1,\sigma_1^2)\),Y服从正态分布\(N(\mu_2,\sigma_2^2)\),X与Y独立,则\(X-Y\)服从\(N(\mu_1-\mu_2,\sigma_1^2+\sigma_2^2)\)的正态分布
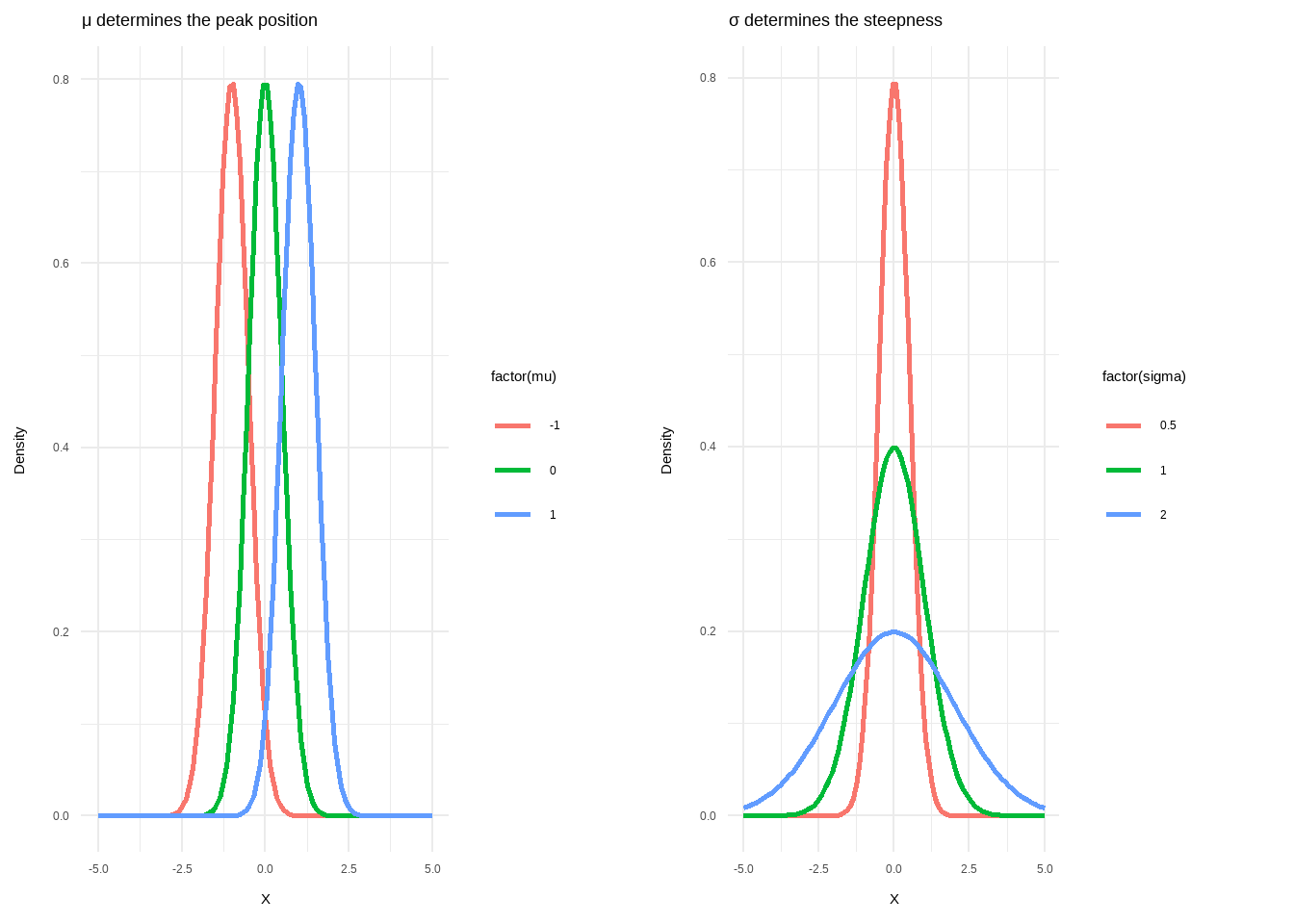
Figure 6.5: Different Normal Curve
6.6 标准正态分布
标准正态随机变量U的密度函数用\(\varphi(u)\)表示,为: \[\varphi(u)=\frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}},(-\infty<x<+\infty)\]
- 标准正态分布(Standard normal distribution):是一种特殊的正态分布,通常用\(U\)或\(Z\)表示服从标准正态分布的变量,此时称随机变量\(X\)服从均数为0,标准差为1的标准正态分布,记为\(X \sim N(0,1)\)
- 正态分布:一簇曲线
- 标准正态分布:一条曲线
- 标准正态变换:Z变换、U变换
- 疑难1:Z值到底表达什么意思?
- 个体值到均值的距离,有多少个标准差 \(Z = \frac{X-\mu}{\sigma}\)
- 只有正态分布的资料才能通过Z变换变成标准正态分布
- 疑难2:标准化变换的公式如何理解?
- 个体值减去均值,除以标准差,均数和标准差由\(\mu,\sigma\)变为\(0,1\)
## TableGrob (1 x 2) "arrange": 2 grobs
## z cells name grob
## 1 1 (1-1,1-1) arrange gtable[layout]
## 2 2 (1-1,2-2) arrange gtable[layout]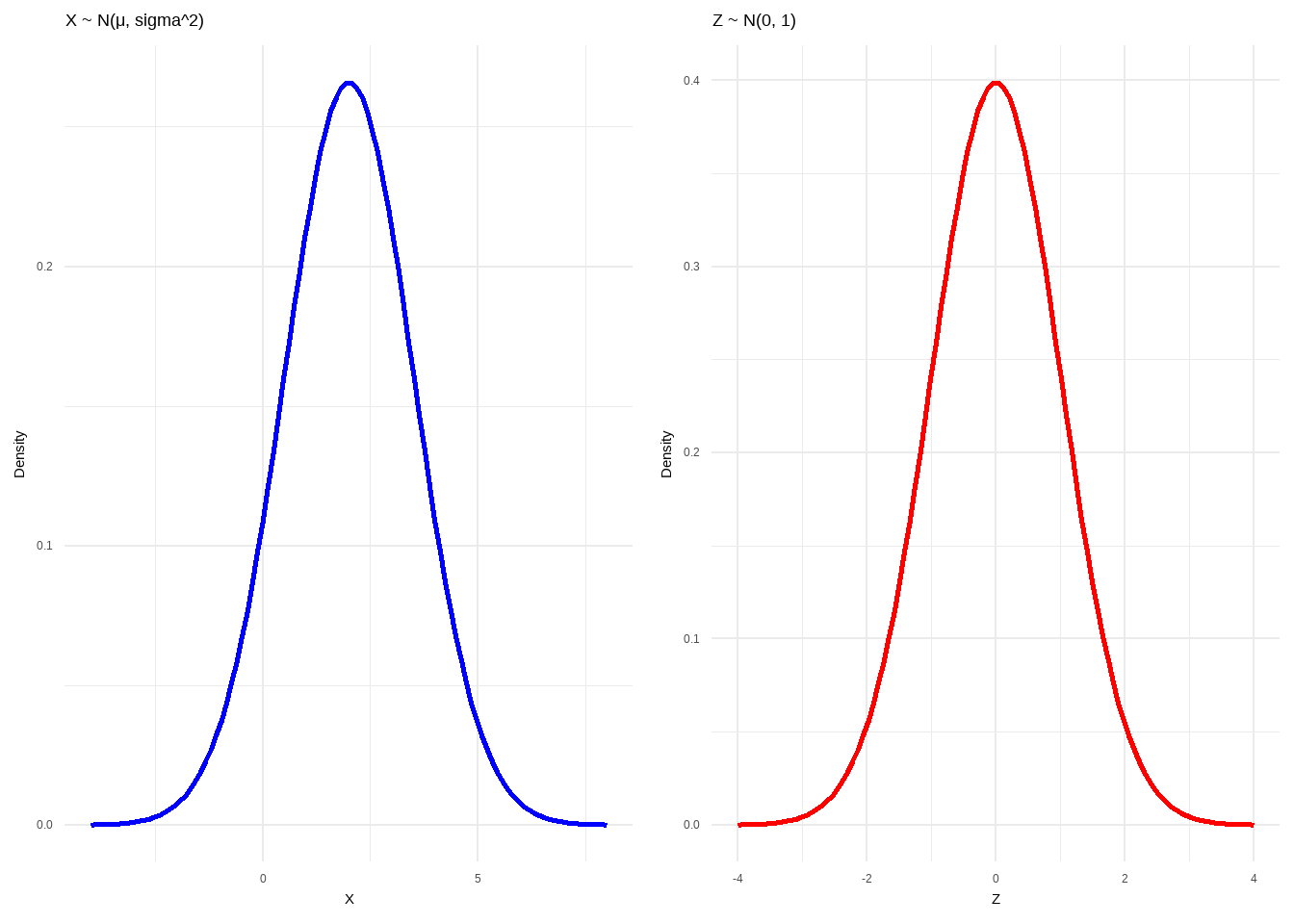
Figure 6.6: Normalized Transformation
6.6.1 正态分布、标准正态分布的应用
- 正态分布的68-95-99.7法则
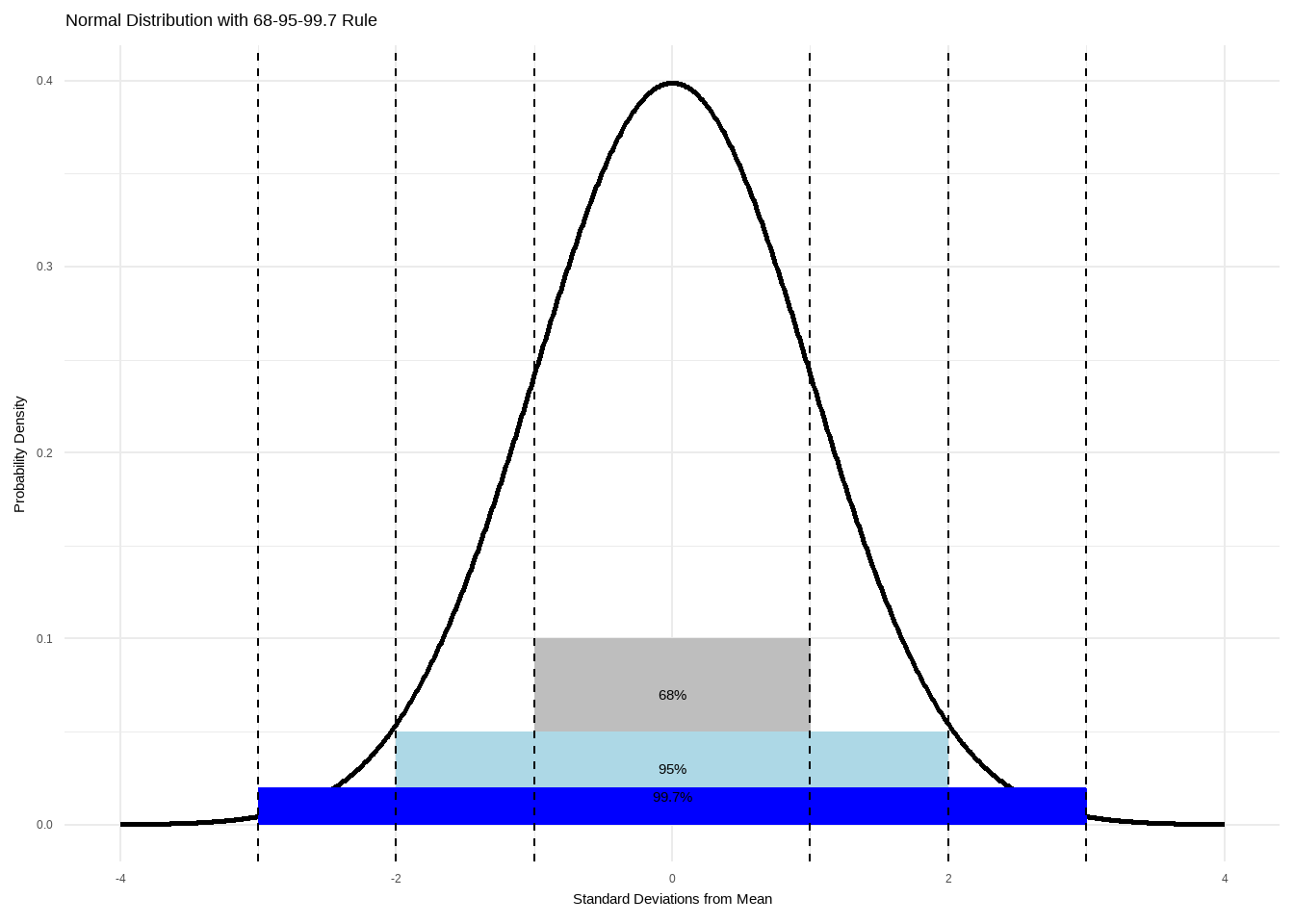
Figure 6.7: Normal
- 标准化转换,涉及到以下两个互逆计算
- 估计某个随机变量在一定取值范围内的观测值个数占全部观测值数量的百分比
- 通过已知的百分比,估计总体变量值的分布范围(本质同医学参考值范围的计算)
- 运用正态近似法计算医学参考值范围
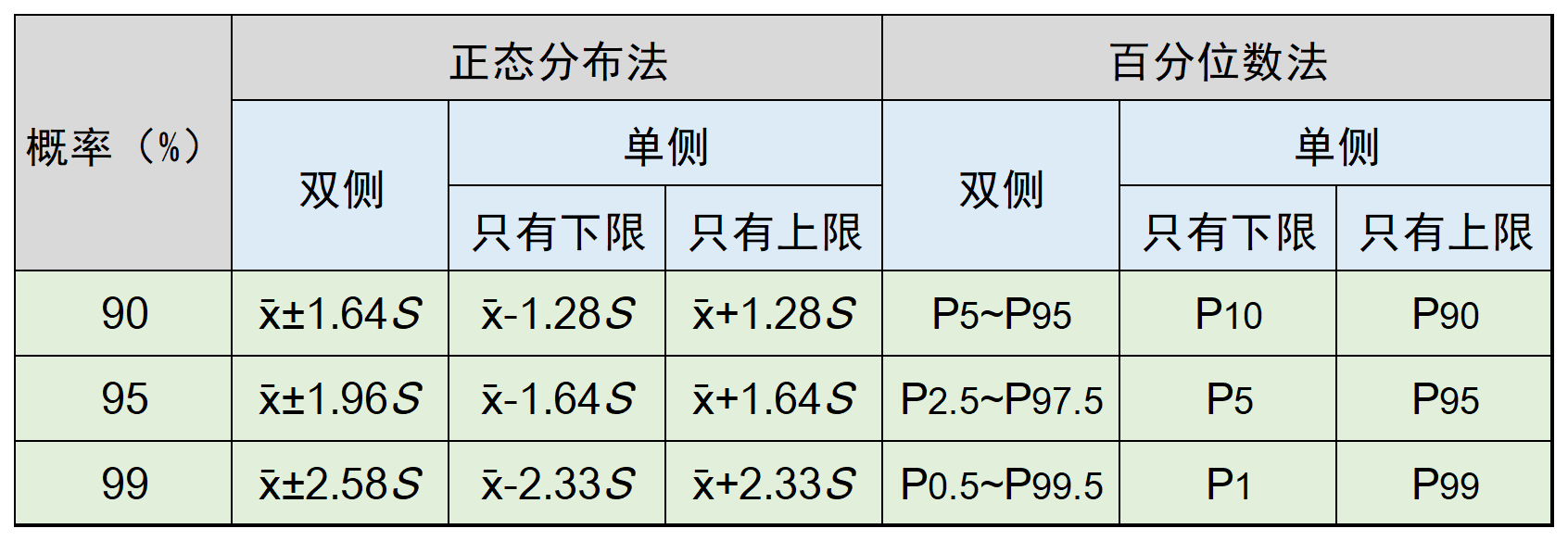
- 运用正态近似法计算置信区间
- 正态分布是很多统计学分析方法的理论基础
notice:
- 正态曲线上的拐点所对应的横坐标为\(\mu ±\sigma\)。
- 设随机变量\(X\)的概率密度曲线为\(f(x)=\frac{1}{2\sqrt{p}}e^{\frac{(x+2)^2}{4}}\),若要将\(X\)转化为服从标准正态分布的变量\(\mu\),则所采用的标准化变换为:\(\frac{X-2}{\sqrt{2}}\)(其原式为:\(f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}\),题目和原式中:\(p=\pi\))