Chapter 12 参数检验
12.1 参数检验和非参数检验的区别
| 维度 | 参数检验(Parameter test) | 非参数检验(Non-parameter tests) |
|---|---|---|
| 定义 | 以特定的总体分布为前提\(\rightarrow\)? | 不依赖于总体分布特征\(\rightarrow\)? |
| 举例 | \(Z\)检验、\(t\)分布、\(F\)检验 | 秩和检验(Rank sum test)、卡方检验 |
| 优点 | 1. 直接利用原始观测值计算统计量,检验效能高; 2.可对总体参数做出估计 |
1. 适用范围广、收集资料方便; 2. 多数非参数检验方法比较简便、易于掌握 |
| 缺点 | 对数据分布有特定要求,适用范围窄 | 1. 没有充分利用原始数据,检验效能低; 2. 不能对总体参数做出推断 |
| 适用范围 | 必须符合相应的要求,如两样本t检验要求:独立、正态、方差齐 | 1. 总体分布形式未知、分布类型不明确、偏态分布数据; 2. 等级资料; 3. 不满足参数检验条件的数据; 4. 数据一段或两端为无法测量的数值等。 |
| 选用原则 | 1. 如果数据符合参数检验条件,或经过变换后符合参数检验的条件,最好用参数检验; 2. 参数检验误用为非参数检验,会导致检验效能降低。 |
12.2 \(t\)分布
| 类目 | \(t\)分布 |
|---|---|
| 概念 | 设从正态分布\(N(\mu,\sigma^2)\)随机抽取含量为n的样本,样本均数为\(\bar x\)、标准差为\(s\)、则\(t=\frac{\bar x-\mu}{s_{\bar x}}=\frac{\bar x-\mu}{s/\sqrt{n}}\),自由度为\(n-1\)。 |
| 图形特点 | 一簇以0为中心,左右对称的单峰曲线; 但随着自由度的增加,\(t\)分布曲线将越来越接近于标准正态分布曲线 |
| 统计量值 | \(t\)的取值范围\(-\infty \sim +\infty\) |
| 自由度 | \(v=n-1\) |
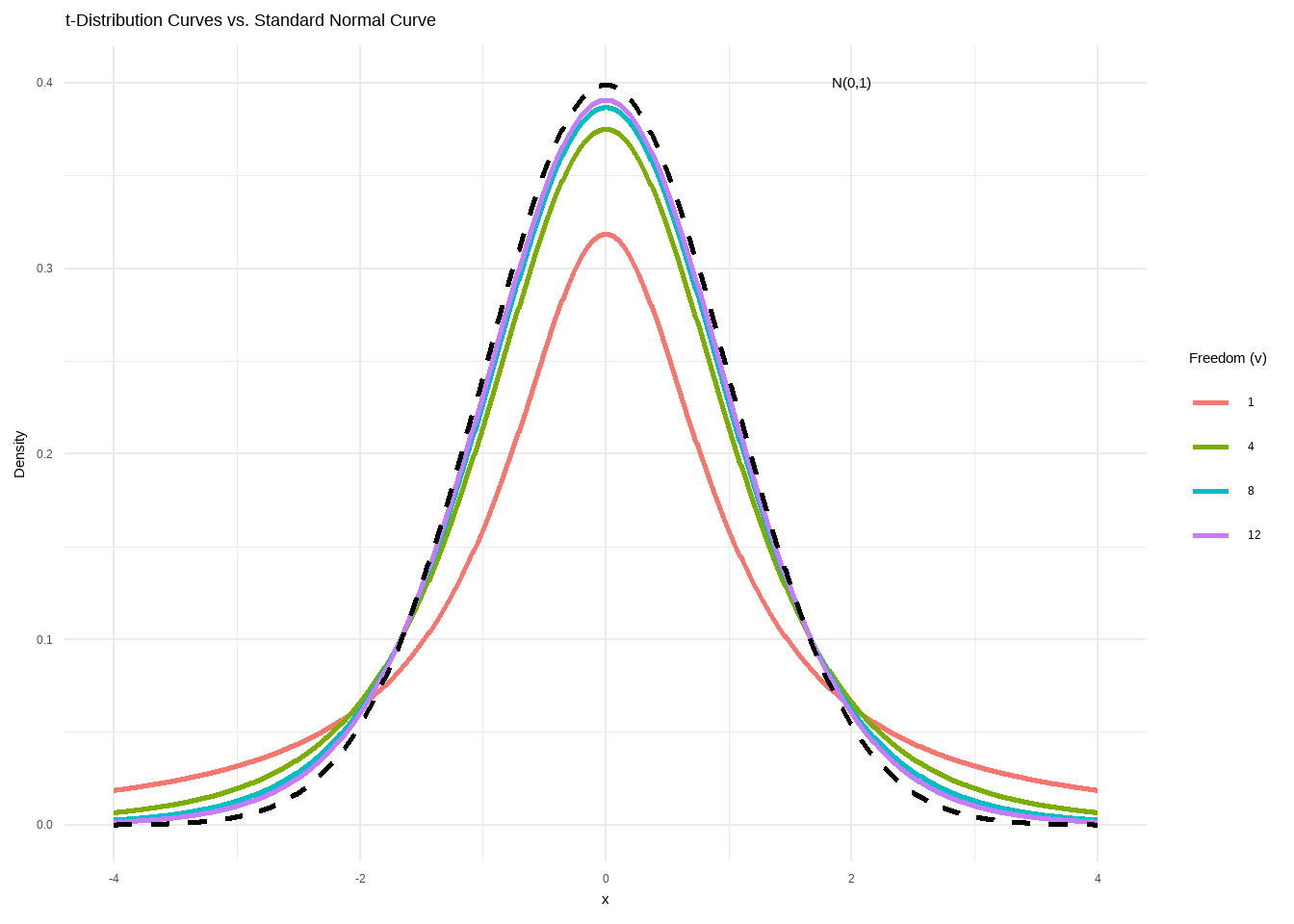
Figure 12.1: t-Distribution Curves vs. Standard Normal Curve
12.3 方差分析
12.3.1 完全随机设计的方差分析
| 类目 | 完全随机设计的方差分析 |
|---|---|
| 数据要求 | 独立性、正态性、方差齐性 |
| 检验目的 | 推断多个样本所代表的总体均数是否不等 |
| \(H_0\)与\(H_1\) | \(H_0\):\(\mu_1=\mu_2=\dots =\mu_a\),各组所代表的总体均数相等。\(H_1\):\(\mu_1,\mu_2,\dots,\mu_a\)各组总体均数不全相等(至少有一个不等式成立) |
| 检验统计量 | \(F=\frac{MS_{组间}}{MS_{组内}}\sim(v_{组间}=k-1,v_{组内}=n-k)\) |
| 关键要点 | 总变异分解为组间变异和组内变异 |
12.3.2 随机区组设计的方差分析
| 类目 | 随机区组设计的方差分析 |
|---|---|
| 数据要求 | 处理组间、区组间数据满足独立、正态性和方差齐性 |
| 处理组假设 | \(H_0\):不同处理组水平的均数相同;\(H_1\):不同处理组水平的均属不全相同 |
| 区组假设 | \(H_0\):不同区组对观测指标的影响很大;\(H_1\):不同区组对观测指标的影响不全相同 |
| 检验统计量 | \(F=\frac{MS_{处理}}{MS_{误差}}\sim(v_{处理}=k-1,v_{误差}=(b-1)×(k-1))\) \(F=\frac{MS_{区组}}{MS_{误差}}\sim(v_{区组}=k-1,v_{误差}=(b-1)×(k-1))\) |
| 关键要点 | 总变异分解为处理组变异、区组变异和随机误差变异 |